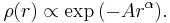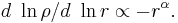Einasto profile

The Einasto profile (or Einasto model or Einasto's law) is a mathematical function that describes how the density $\rho$ of a spherical stellar system varies with distance $r$ from its center. Jaan Einasto introduced his model at a 1963 conference in Alma-Ata, Kazakhstan.^[1]

The Einasto profile has the form

$\rho(r) \propto \exp{(-Ar^\alpha)} .$

The parameter $\alpha$ controls the degree of curvature of the profile. This can be seen by computing the slope on a log-log plot:

$d\ \ln\rho/d\ \ln r \propto -r^{\alpha} .$

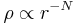The larger $\alpha$ , the more rapidly the slope varies with radius (see figure). Einasto's law can be described as a generalization of a power law, $\rho\propto r^{-N}$ , which has a constant slope on a log-log plot.

Einasto's law has the same mathematical form as Sersic's law, which is used to describe the surface brightness (i.e. projected density) profile of galaxies.

Einasto's model has been used to describe many types of system, including galaxies^[2] and dark matter halos.^[3]

References

^ J. Einasto (1965), Kinematics and dynamics of stellar systems, Trudy Inst. Astrofiz. Alma-Ata 51, 87
^ J. Einasto and U. Haud (1989), Galactic models with massive corona. I - Method. II - Galaxy Astron. Astrophys. 223, 89
^ D. Merritt et al. (2006), Empirical Models for Dark Matter Halos. I. Nonparametric Construction of Density Profiles and Comparison with Parametric Models Astron. J. 132, 2685

External links

Spherical galaxy models with power-law logarithmic slope. A comprehensive paper that derives many properties of stellar systems obeying Einasto's law.